Siguiendo con el tema de los arrays ahora toca el turno a los arreglos bidimensionales, también conocidos como matrices o tablas.

Cabe hacer notar que este tipo de arreglo es quizá el tipo más utilizado dentro de las estructuras de datos más básicas ya que permite mapear datos en filas y columnas. El ejemplo más clásico que me viene a la mente en este momento es cuando queremos manejar las calificaciones de un grupo, las filas serían los alumnos, mientras que las columnas representarían las calificaciones de cada uno de los periodos de evaluación, y la última columna podría ser el promedio final.

Nombres	C1	C2	C3	PF
Luis	7.8	9.3	8.6	8.56
Lorena	9.5	4.5	7.6	7.2
Norma	8.9	2.6	9.9	7.13

Así pues construir mediante código un programa que haga la simulación de esta tabla de calificaciones y que permita realizar los cálculos es muy sencillo utilizando C#, sin embargo, se deben comprender perfectamente bien los fundamentos del manejo de los arreglos de dos dimensiones antes de pasar a cosas más complejas.

Para ello vamos a realizar un ejercicio que permita aclararnos algunos puntos esenciales a la hora de manejar matrices en C#.

Primero debemos de notar que la declaración de una matriz se hace de la forma:

int[ , ] matriz = new int[5,3];

donde notamos que la declaración comienza por indicar el tipo de dato de los valores que contendrá la matriz seguido de un par de corchetes con una coma en medio, esto indica que habrán dos valores de tamaños, tal como después se muestra utilizando el 5 y el 3, esto significa, que la matriz tendrá 5 filas y 3 columnas.

Ahora bien, análogamente a como sería el proceso para llenar con un valor un vector donde se usa un solo ciclo for, para una matriz requerimos dos ciclos for anidados para recorrer todos los espacios de memoria que conforman nuestra tabla.

Aquí cabe resaltar algo importante, aunque gráficamente se tenga la concepción de que una matriz es una tabla de filas y columnas, en la memoria de la computadora no existe tal representación, sino que solo son localidades de memoria consecutivas, siguiendo la regla que ya se explicó en el post anterior.

Entonces si por ejemplo queremos llenar toda la matriz con 8, los ciclos quedarían algo así:

//llenar la matriz con valores
            for (int i = 0; i < matriz.GetLength(0); i++)
            {
                for (int j = 0; j < matriz.GetLength(1); j++)
                {
                    matriz[i, j] = 8;
                }
            }

De esto debemos observar que ahora para extraer el numero de elementos de cada dimensión se ocupa la instrucción GetLength(valor), y el valor que lleva entre los paréntesis es la dimensión a la que queremos acceder, siendo en este caso 0 para las filas y 1 para las columnas.

Entonces el código completo de nuestra clase Arreglo quedaría así:

class Arreglo
    {
        //zona de atributos

        //zona de métodos
        public void ArregloBidimensional()
        {
            //declaracion del arreglo bidimensional
            int[,] arrayBidi = new int[10, 8];

            //llenar la matriz con valores 8 e imprimir la matriz
            for (int i = 0; i < arrayBidi.GetLength(0); i++)
            {
                for (int j = 0; j < arrayBidi.GetLength(1); j++)
                {
                    arrayBidi[i, j] = 8;
                    Console.Write("[" + arrayBidi[i, j] +
                        "|" + i + "," + j + "] ");
                }
            }
        }
     }

 Y el main en la clase Program sería:

class Program
    {
        static void Main(string[] args)
        {
            Arreglo arregloBidi = new Arreglo();

            arregloBidi.ArregloBidimensional();

            Console.ReadKey();
        }
    }

 Y la salida después de ejecutar el programa sería esta:

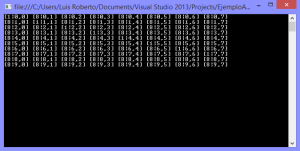
Es de notar que estoy utilizando el mismo tipo de formato para la impresión que en el ejemplo de manejo de vectores, donde los 8 son el valor de cada posición en la tabla y el par ordenado que le sigue a los dos puntos son los indices de la posición de cada valor en la matriz.

Hasta aquí este post que espero les sea de utilidad.